Simple Harmonic Motion (SHM)
Cut to the Chase
Introduction
In addition to linear motion and rotational motion there is another kind of motion that is common in physics. This is the to and fro motion of oscilations or vibrations.
When something oscillates, it moves back and forth with time. It is helpful to trace out the position of an oscillating particle with time so we can define some terminology.
Period, Amplitude and Frequency
The time taken for the particle to complete one oscilation, that is, the time taken for the particle to move from its starting position and return to its original position is known as the period. and is generally given the symbol T. The frequency ν is related to the period, it is defined as how many oscillations occur in one second. Since the period is the time taken for one oscillation, the frequency is given by
The frequency is measured in [s-1]. This unit is known as the Hertz (Hz) in honour of the physicist Heinrich Hertz. The maximum displacement of the particle from its resting position is known as the amplitude. The frequency is also given the symbol f.
Simple Harmonic Motion
The definition of simple harmonic motion is simply that the acceleration causing the motion a of the particle or object is proportional and in opposition to its displacement x from its equilibrium position.
a(t) ∝ -x(t)
Where k is a constant of proportionality. This remembering that the acceleration is the second derivative of position, also leads us to the differential equation
x''(t) = - k x(t)
Simple Harmonic Motion is closely related to circular motion as can be seen if we take an object that moves in a circular path, like a ball stuck on a turntable. If we consider just the y-component of the motion the path with time we can see that it traces out a wave as shown in Flash 2.
We can also see that the period of the motion is equal to the time it takes for one rotation. Therefore, if we know the angular velocity ω = &theta/t. For one rotation, ω = 2π/T therefore the period is also equal to
The particle can also at different speeds is conected with the period. The frequency is the number of oscilations per second.
Consider the particle undergoing simple harmonic motion in Flash 3. The displacement with time takes the form of a sinusoidial wave. The velocity of the particle can be calculated by differentiating the displacement. The result is also a wave but the maximum amplitude is delayed, so that when the displacement is at a maximum the velocity is at a minimum and when the displacement is zero the velocity has its greatest value.
Simple Harmonic Motion is characterised by the acceleration a being oppositely proportional to the displacement, y.
We set this out mathematically, using a differential equation as in equation (4). We specify the equation in terms of the forces acting on the object. The acceleration is the second derivative of the position with respect to time and this is proportional to the position with respect to time. The minus sign indicates that the position is in the opposite direction to the acceleration.
The derivation of the solution can be found here
For which the general solution is a wave like solution.
y(t) = c1 cos(ωt) + c2 sin(ωt)
Where, ω is the angular frequency. (ω=2πf) The values of c1 and c2 are determined by the initial conditions. Specifically, c1 = y0 and c2 = v0/ω These two initial conditions specify the starting position and the initial velocity.
The general solution can also be written more compactly as
y(t)= A cos(ωt - φ)(5)
Where φ = tan-1(ωy0/v0), A = (y02 + (v0/ω)2)1/2
Differentiating once with respect to time, we obtain the velocity. (The derivative of cos x = - sin x)
Finally, the acceleration is the derivative of the velocity with respect to time. (The derivitive of -sin x = - cos x)
Substituting equations (5) and (7) into equation (4) we verify that this does indeed satisfy the equation for simple harmonic motion. With the constant of proportionality k = ω2
Thus
a(t) = - ω2y(t)
The time for the maximum velocity and acceleration can be determined from these equations. From equation (6) the maximum magnitude of the velocity occurs when sin(ωt - φ) is 1 or -1. Therefore the maximum velocity is ±ωA. Intuitively, we can imagine that this velocity occurs when the oscillating system has reached the equilibrium position and is about to overshoot. The minus sign indicates the direction of travel is in the opposite direction.
The maximum acceleration occurs where the argument of cosine in eqn (7) is also -1 or 1. Thus the maximum acceleration is ±ω2A which occurs at the ends of the oscillations, as this is where the direction changes.
Examples of SHM
Spring Mass System
Consider a spring of spring constant k conected to a mass m. If the mass is displaced from its equilibrium position by a distance x a force F will act in the opposite direction to the displacement. From Hooke's Law the magnitude of the force is given by
F= - k x
When the mass is released it the force will act on the mass to bring it back to its equilibrium position. However, if there is no friction the inertia of the mass will cause it to overshoot the equilibrium position and the force will act in the opposite direction slowing it down and pulling it back.
The action of this force on the mass keeps it oscillating backwards and forwards.
The spring mass system consists of a spring with a spring constant of k attached to a mass, m.The mass is displaced a distance x from its equilibrium position work is done and potential energy is stored in the spring. If the mass is displaced by a small distance dx, the work done in stretching the spring is given by dW = F dx.
The force on the spring is assumed to obey Hooke's law, therefore, the restoring force is proportional to the extension. The work done is then dW = - k x dx
Making the total work W = - ∫k x dx = -1/2 k x2 + C
At the time of release, the energy of the system will consist totally of potential energy. PE= -1/2 kx2 and the potential energy as a function of time is
PE(t) = 1/2k A cos2(ωt - φ)
As the spring pulls the mass toward the equilibrium position, the potential energy is transformed into kinetic energy until at the equilibrium position the kinetic energy will be maximised. The KE is 1/2 mv2 and the maximum velocity occurs at x=0. From equation (6), the velocity will be ω A
Therefore the kinetic energy is 1/2 mω2A2 sin2(ωt - φ)
From the conservation of mechanical energy, the sum of energy between kinetic energy and potential energy will always be the same.
U = KE(t) + PE(t) = 1/2 mω2A2 sin2(ωt - φ) + 1/2k A cos2(ωt - φ)
1/2mω2x2 = 1/2k x2
is transferred into kinetic energy by moving the mass. For a particle undergoing simple harmonic motion, the displacement x is given by equation 1. The potential energy is gradually transferred to kinetic energy. Kinetic energy is given by 1/2 mv2. The velocity is given by equation (6). Summing the kinetic energy and potential energy we obtain,
= 1/2 k A2(8)
Since k = mω2 and cos2x + sin2x = 1
Flash 5 shows the change in energy betweeen kinetic energy and potential energy with time. The blue line shows the potential energy. It is highest at the positions of maximum displacement. The red line shows the kinetic energy. It has a maximum when the velocity is greatest, ie. as it passes the equilibrium position. The green line shows the total mechanical energy of the system, ie. the sum of the potential energy and kinetic energy. The total energy remains constant because there are no losses to friction, heat or air resistance.
Simple Pendulum
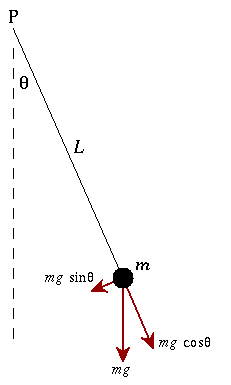
Another common example used to illustrate simple harmonic motion is the simple pendulum. This idealised system has a one end massless string suspended a mass m and the other end fixed to a stationary point. If the mass is displaced by a small distance, the angle moved is small.
The torque on the fixed point P is τ = Iα
- mg sin θ(t)L = mL2 θ''(t)
θ''(t) +g/L θ(t) = 0
This has the same form as simple harmonic motion equation, x''(t) - ω2 x(t), and so the solution is θ(t) = θ0 cos(ωt - &phi)
the angular frequency is ω = (g/L)1/2.
It is interesting to note that the mass does not appear in this equation. This means that the frequency of the period only depends on the length of the string and the force of gravity. Pendulums with shorter strings will oscillate faster than pendulums with longer strings. And the same pendulum on the moon, where the force of gravity is 1/6th that of the gravity on the Earth, will also take longer to oscillate.
We have glossed over one important aspect, in that this analysis is true only for small angles of theta. We had to make the approximation that sin θ is aproximately the same as θ which is true only for small angles. The real differential equation
θ''(t) +g/L sin θ(t) = 0
is non-linear and cannot be solved analytically.
Torsional Pendulum
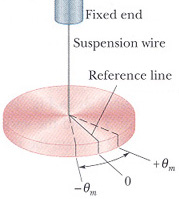
A mass suspended to a fixed support by a thin wire can be made to twist about its axis. This is known as a torsional pendulum. The mass attached to the wire rotates in the horizontal plane. In this case θ is the angle of rotation. When the wire is untwisted and in equilibrium, the angle θ is 0 degrees. It is the twisting of the wire that creates a restoring torque due to the resistance of the wire to the deformation. For small angles of θ the magnitude of the torque is proportional to the angle θ
τ = - k θ
Where k is the torque constant of the wire. As with the simple pendulum the equation of motion is
τ = Iα
Where I is the moment of inertia
kθ(t) = - Iθ''(t)
Once again we have formed the equation for simple harmonic motion and can write the solution as θ(t) = A cos(ωt - φ)
The angular frequency, ω is given by
ω = (k/I)1/2
Summary
An oscillation follows simple harmonic motion if it fulfils the following two rules:
- Acceleration is always in the opposite direction to the displacement from the equilibrium position
- Acceleration is proportional to the displacement from the equilibrium position
The acceleration and displacement are linked by the following equation:
a(t) = - ω2 x(t)Here ω is called the angular frequency of oscillation, and is given by 2π /T or 2π f
T is the period of oscillation (s), f=1/T = frequency of oscillation (Hz) and x is the displacement (m).
Using Newton's 2nd Law (F=ma) we can show that the Force on the object due to inertia will be:
F= -mω2 x
Using Hooke's Law for springs (F=-kx), we know that the force on the oscillating mass due to the springs is simplyF=-kx
These two forces are always in balance, so m ω2 x - kx = 0
From this we can find the resonant frequency:
ω2=(kx) / (mx) = k/m,
ω = (k/m)1/2
f = 1/ 2π * [(k/m)1/2]
