Keplers Laws
Introduction
Tyco Brahe was a Danish nobelman born in 1546. Over a 20 year period of time, from his island, Hven, Tycho Brahe made consistent observations which supported the heliocentric theory proposed earlier by Copernicus. Brahe lived before the invention of the telescope and so these observations were made using only a compass and a sextant. Despite the lack of a telescope his acheivements were many. Brahe catalogued over 1000 stars. He also proved that comets were not just components of Earth's atmosphere, but actual objects traveling through space. Brahe showed irregularities in the Moon's orbit and discovered a new star in the Cassiopeia formation. Brahe invented many instruments such as the Tyconian Quadrant which were widely copied and led to the invention of improved observational equipment.
He is also well known for several quirky anecdotes. Brahe had his nose badly cut in a dual in December 1566, and had a replacement nose made from an alloy of gold and silver. Another famous story is about how he had a tame moose. His mentor the Landgraf Wilhelm of Hesse-Kassel asked about an animal faster than a deer. Tycho replied writing there were none, but he could send his tame moose. However, Wilhelm never got his moose. Tycho replied later with the sad news that the moose had died on a visit to entertain a nobleman at Landskrona. Apparently, during dinner the moose had drunk a lot of beer and fell down the stairs and died.
Brahe was hired by Emperor Rudolph II, who believed in astrology. As was common for astronomers at this time, Brahe's task was to calculate a list of days which were especially unlucky, when it was best to do nothing important at all. The Tyco Brahe calendar lists 33 so called Tykobrahe days.
Brahe Model of the Universe
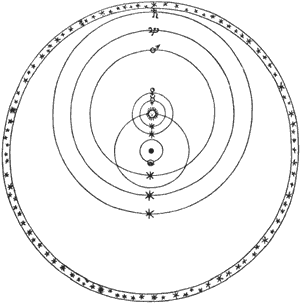
Brahe's model of the universe was a compromise between the geocentric and heliocentric models. He believed the Earth was at the centre of the universe and the Sun and Moon orbited the Earth, while the planets orbited the Sun as shown in Figure 1.
In 1600, Tyco Brahe hired Johannes Kepler as his assistant. In later years, Kepler would use Brahe's work as the basis for the laws of planetary movement which he developed. Brahe did not live long enough to see the successes of Kepler, and even if he had, he might not have been very pleased with the result as he believed the Earth was at the centre of the Universe. Tyco Brahe died at a dinner in 1601. It is often said that his death was the result of bladder complications because he did not go to the toilet out of respect for the host, but in fact recent studies have shown that he probably died as a result of Mercury poisoning.
Kepler's Laws
Johannes Kepler, painstakingly analysed the observations of the motion of the planets made by Tycho Brahe. Kepler had been trained as a Platonist and Neo-pythagorean, and was given to rather mystical views, as exemplified in his work Mysterium Cosmographicum. Nevertheless, Kepler was also a confirmed Copernican. In fact, he wanted to use Tycho's data to prove the validity of the Copernican theory. He analyzed the vast amount of data upon Brahe's death. From this data, he prepared new planetary tables (called the Rudolphine Tables). Kepler tried all sorts of mystical notions to describe planetary orbits, using the Platonic solids and musical analogies. The first two laws were published in his voluminous calculations in Astronomia Nova (New Astronomy) while the third law followed in his fifth book, Harmonices mundi libri V (Harmony of the World). It is also interesting to note he was able to draw his conclusions because he happened to be observing Mars, the only planet visible to the naked eye with an eccentricity large enough so as to allow one to distinguish its elliptical orbit from a circular one with the rudimentary observation instruments available at the time. For the formulation of these laws, Kepler is considered the founder of physical astronomy.
Kepler's 1st Law
the planets move in elliptical orbits with the Sun at one focus.
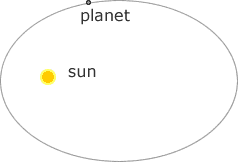
Figure 2. Elliptical orbit of planet around the Sun
Generally, there is nothing in the other focus of the ellispe. Strictly, speaking both the Sun and the planet move around each other. However, as the Sun is much more massive than the planet that is orbiting around it, the Sun is essentially fixed in space.
Kepler's 2nd Law
The planets sweep out equal areas in equal times (which is equivalent to the statement of conservation of angular momentum.
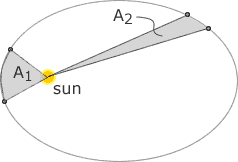
Figure 3. Equal areas are swept out in equal times. A1=A2
The fact that equal areas are swept out in equal times is a restatement of the conservation of angular momentum. To see why consider Figure 4,
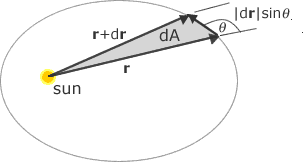
Figure 4. Conservation of angular momentum of planet around the Sun.
which shows an infinitesimal area dA which is swept out in in infinitesimal time interval dt. The area is that of a triangle of height |dr|=sin θ and base r.
dA=1/2r|dr| sin θ =1/2 rv dt sin θ
where we have used |dr| = v dt. Dividing both sides by dt and multiplying and dividing the right-hand side by m gives,
dA/dt=(mvr sin θ)/(2m)
Where the numerator of this expression is the angular momentum mvr.
Kepler's 3rd Law
The third law states that the period T squared is proportional to the semimajor axis r cubed. T2 ∝ r3
Newton was able to derive the third law using the universal law of gravitation
