Binding Energy Curve
The mass of a nucleus is less than the sum of it constituent protons and neutrons. If we took the same number of protons and neutrons as in the nucleus we were trying to recreate, we would find the total mass of the individual protons and neutrons is greater than when they are arranged as a nucleus. The difference in mass between the products and sum of the individual nucleons is known as the mass defect. The binding energy is the amount of energy required to break the nucleus into protons and neutrons again; the larger the binding energy, the more difficult that would be. Figure. 1. Shows the binding energy for each element, against their atomic number.
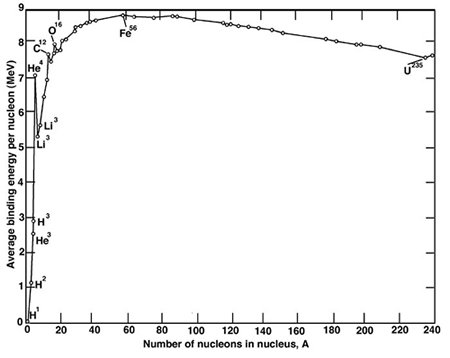
Starting from Hydrogen, as we increase the atomic number, the binding energy increases. So Helium has a greater binding energy per nucleon than Hydrogen while Lithium has a greater binding energy than Helium, and Berilium has a greater binding energy than Lithium, and so on. This trend continues, until we reach iron. It begins to decrease slowly.
The binding energy curve is obtained by dividing the total nuclear binding energy by the number of nucleons. The fact that there is a peak in the binding energy curve in the region of stability near iron means that either the breakup of heavier nuclei (fission) or the combining of lighter nuclei (fusion) will yield nuclei which are more tightly bound (less mass per nucleon).
The binding energy is intimately linked with fusion and fission. The lighter elements up to Fe are available will release energy via the fusion process, while in the opposite direction the heaviest elements down Fe are more susceptable to liberate energy via fission.
